RELASI DAN FUNGSI

Assalamualaikum Warahmatullahi Wabarakatuh,

RELASI

1.1 Pengertian Relasi

Relasi adalah Anggota sebuah himpunan dapat dihubungkan dengan anggota himpunan lain atau dengan anggota himpunan yang sama.

Contoh 

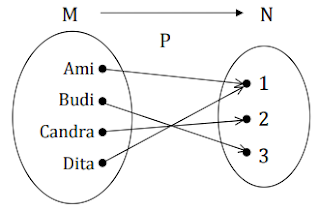
misalkan M = {Ami,Budi,Candra,Dita} dan N = {1, 2, 3}. Misalkan pula, Ami berusia 1 tahun, Budi berusia 3 tahun, Candra berusia 2 tahun dan Dita berusia 1 tahun, maka kita dapat menuliskan sebuah himpunan P = {(Ami, 1), (Budi, 3), (Candra, 2), (Dita, 1)} dimana P merupakan himpunan pasangan terurut yang menggambarkan hubungan antara himpunan M dengan himpunan N. Himpunan P merupakan relasi antara himpunan M dengan himpunan N dan dapat ditulis sebagai P = {(x,y) | x berusia y, dimana xÎM dan yÎN}.

1.2 Penyajian Relasi

Sebuah relasi dapat disajikan dalam beberapa bentuk, yaitu :

1. Himpunan pasangan terurut dalam bentuk pendaftaran (tabulasi), P = {(Ami, 1), (Budi, 3), (Candra, 2), (Dita, 1)}

2. Himpunan pasangan terurut dalam bentuk pencirian, P = {(x,y) | x berusia y, dimana xÎM dan yÎN}

3. Diagram panah,

4. Diagram koordinat atau grafik relasi,

5. Matriks relasi,

6. Bentuk graf berarah (digraf),

• Relasi pada sebuah himpunan dapat direpresentasikan secara grafis dengan graf berarah (directed graph atau digraph).
• Graf berarah tidak didefinisikan untuk merepresentasikan relasi dari suatu himpunan ke himpunan lain. 
• Tiap elemen himpunan dinyatakan dengan sebuah titik (disebut juga simpul atau vertex), dan tiap pasangan terurut dinyatakan dengan busur (arc).

Contoh

7. Relasi dengan tabel,

• Kolom pertama tabel menyatakan daerah asal, sedangkan kolom kedua menyatakan daerah hasil.  

1.3 Sifat Sifat Relasi Biner

• Relasi Biner yang didefinisikan pada sebuah himpunan mempunyai beberapa sifat. 

1. Refleksif

Misalkan R sebuah relasi yang didefinisikan pada himpunan A. Relasi R.

jika untuk setiap a  Î A berlaku (a,a) Î R. Contoh :

• Diketahui A = {1, 2, 3}. Pada A didefinisikan relasi R1 = {(1,1), (1,2), (2,2), (2,3) , (3,3) , (3,2)}. Relasi R1 tersebut bersifat refleksif. 
• Diketahui B = {2,4,5}. Pada B didefinisikan relasi R2 = {(x,y) | x kelipatan y, x, y  Î B}. Maka R2 = {(2,2), (4,4), (5,5), (4,2)}. Relasi R2 tersebut bersifat refleksif. 
• Diketahui B = {2,4,5}. Pada B didefinisikan relasi R3 = {(x,y) | x + y <10, x,y Î A}. Maka R3={(2,2), (2,4), (2,5), (4,2), (4,4), (4,5), (5,2), (5,4)}. Relasi R3 tersebut tidak bersifat refleksif. 

2.Simetris

Relasi R bersifat simetris jika untuk setiap (a,b)  Î R berlaku (b,a)  Î  R. Contoh :

• Diketahui A = { 1, 2, 3 }. Pada A didefinisikan relasi R4 = {(1,1) , (1,2) , (2,2) , (2,1) , (3,3)}. Relasi R4 tersebut bersifat simetris. 
• Diketahui B = { 2, 4, 5 }. Pada B didefinisikan relasi R5 = { (x,y)  |  x kelipatan y , x, y  Î  B } = {(2,2) , (4,4) , (5,5) , (4,2)}. Relasi R5 tersebut tidak bersifat simetris karena (4,2)  Î  R5 tetapi (2,4) Ï R5.

3. Transitif

Relasi R bersifat transitif, jika untuk setiap (a,b)ÎR dan (b,c)ÎR berlaku (a,c)ÎR. Contoh :

• Diketahui A = { 1, 2, 3 }. Pada A didefinisikan relasi R6 = {(1,1) , (1,2) , (2,2) , (2,1) , (3,3)} Relasi R6 tersebut bersifat transitif. 
• Relasi R7 = {(1,1) , (1,2) , (2,2) , (2,3) , (3,3) , (3,2)} yang didefinisikan pada himpunan A = {1, 2, 3 } tidak bersifat transitif, karena terdapat (1,2) Î R7 dan (2,3) Î R7, tetapi (1,3) Ï R7.

4. Antisimetris

Relasi R dikatakan bersifat antisimetris jika untuk setiap (a,b) Î R dan (b,a) Î R berlaku a = b. Contoh :

• Pada himpunan B = { 2, 4, 5 } didefinisikan relasi R8 = { (x,y) | x kelipatan y , x,y Î B }. Dengan demikian R8 = {(2,2),(4,4),(5,5),(4,2)}. Relasi R8 tersebut bersifat antisimetris.
• Diketahui A = { 1, 2, 3 }. Pada A didefinisikan relasi R9 = { (1,1) , (1,2) , (2,2) , (2,1) , (3,3) } Relasi R9 tersebut tidak bersifat antisimetris karena terdapat (1,2)ΠR9 dan (2,1) Î R9, tetapi 1 tidak sama dengan 2.

RELASI EKIVALEN 

Relasi R disebut sebagai sebuah relasi ekivalen jika relasi tersebut bersifat refleksif, simetris dan transitif. Contoh :  

• Diketahui A = { 1, 2, 3 }. Pada A didefinisikan relasi R1 = { (1,1) , (1,2) , (2,2) , (2,1) , (3,3) } Relasi R1 tersebut bersifat refleksif, simetris dan transitif. Oleh karena itu relasi R1 merupakan relasi ekivalen. 
• Diketahui B = { 2, 4, 5 }. Pada B didefinisikan relasi R2 = { (x,y) | x kelipatan y , x, y Î B } maka R2 = { (2,2) , (4,4) , (5,5) , (4,2) }. Relasi R2 tersebut tidak bersifat simetris, oleh karena itu relasi tersebut bukan relasi ekivalen.

RELASI PENGURUTAN SEBAGIAN (PARTIAL ORDERING) 

Relasi R disebut sebagai sebuah relasi pengurutan sebagian (partial ordering), jika relasi tersebut bersifat refleksif, transitif dan antisimetris. 

Contoh 20 Diketahui A = { 1, 2, 3 }. Pada A didefinisikan relasi R3 = { (1,1) , (1,2) , (2,2) , (2,1) , (3,3) }. Relasi R3 tersebut bersifat refleksif dan transitif, tetapi tidak bersifat antisimetris. Oleh karena itu relasi tersebut bukan merupakan relasi pengurutan sebagian. 

Contoh 21 Diketahui B = { 2, 4, 5 }. Pada B didefinisikan relasi R4 = { (x,y) | x kelipatan y , x,y Î B } maka R4 = { (2,2) , (4,4) , (5,5) , (4,2) }. Relasi R4 tersebut bersifat refleksif, antisimetris dan transitif. Oleh karena itu relasi tersebut merupakan relasi pengurutan sebagian.

FUNGSI

2.1 Definisi Fungsi

Misal f adalah relasi dari A ke B. f disebut fungsi jika untuk setiap anggota A direlasikan dengan tepat satu anggota B. 

Contoh: Misal A = {1,2,3}, B = {u,v,w} 

1. f = {(1,u),(2,v),(3,w)} adalah fungsi 

2. f = {(1,u),(2,u),(3,w)} adalah fungsi.

2.2 Jenis Fungsi 

• Fungsi f disebut satu satu / injectif ,jika tidak ada elemen himpunan A yang mempunyai bayangan yang sama atau untuk setiap a,b∈A, jika a ≠ b maka f(a) ≠ f(b). 

Contoh: f = {(1,w),(2,u),(3,v)} 

• Fungsi f dikatakan pada / onto / surjektif, jika setiap anggota himpunan B adalah merupakan bayangan dari satu atau lebih anggota himpunan A. 

Contoh: f = {(1,w),(2,u),(3,v)} 

• Fungsi f dikatakan berkoresponden satu – satu / bijektif jika f adalah fungsi satu satu dan pada.

Gambar berikut akan memperlihatkan perbedaan fungsi, fungsi satu – satu, fungsi pada.

Waalaikumsalam Warahmatullahi Wabarakatuh,

Semoga bermanfaat ya guys:)

HIMPUNAN

Assalamualaikum Warahmatullahi Wabarakatuh

Salam kenal:)

HIMPUNAN

1.1 Pengertian Himpunan

Himpunan adalah kumpulan benda (objek). Pernahkah kamu memperhatikan benda-benda yang ada di rumahmu?. Jika kamu perhatikan, ternyata di rumahmu terdapat beberapa kumpulan benda yang jelas batasannya, antara lain:

1. sepatu

2. gelas

3. alat-alat elektronik

4. keluarga

5. kursi, dan sebagainya.

Jadi, dapat disimpulkan bahwa  Suatu kumpulan benda (objek) tertentu dengan batasan yang jelas dalam matematika disebut himpunan.

1.2 Cara Penulisan Himpunan

1. Enumerasi                                                                                                                

Mengenumerasi artinya menuliskan semua elemen himpunan yang bersangkutan di antara dua buah tanda kurung kurawal. Biasanya suatu himpunan diberi nama dengan menggunakan huruf  kapital maupun dengan menggunakan simbol-simbol lainnya. 

Contoh :

-  misalkan X ialah himpunan hewan berkaki 4,  X = {kuda,anjing,sapi}

-  Himpunan empat bilangan asli pertama: A = {1, 2, 3, 4}.     

-  Himpunan lima bilangan genap positif pertama: B = {4, 6, 8, 10}.

-  C = {kucing, a, Amir, 10, paku} 

-  R  = { a, b, {a, b, c}, {a, c} }

-  C  = {a, {a}, {{a}} }

-  K  = { {} }                                     

-  Himpunan 100 buah bilangan asli pertama: {1, 2, ..., 100 }      

-  Himpunan bilangan bulat ditulis sebagai {…, -2, -1, 0, 1, 2, …}.

2. Simbol - Simbol Baku
Penulisan himpunan yang sudah baku dikhususkan bagi himpunan yang telah baku dan sering digunakan dalam penjabaran matematika.

Contoh :

P =  himpunan bilangan bulat positif  =  { 1, 2, 3, ... }

N =  himpunan bilangan alami (natural)  =  { 1, 2, ... }

Z =  himpunan bilangan bulat  =  { ..., -2, -1, 0, 1, 2, ... }

Q =  himpunan bilangan rasional

R =  himpunan bilangan riil

C =  himpunan bilangan kompleks

Terdapat penulisan simbol Himpunan dalam bentuk Universal atau biasa disebut Himpunan Semesta, disimbolkan dengan U.

Misalkan U = {1, 2, 3, 4, 5} dan A adalah himpunan bagian dari U, dengan A = {1, 3, 5}.

3. Notasi Pembentuk Himpunan
Penulisan notasi adalah { x | syarat yang harus dipenuhi oleh x }

Contoh  :
A adalah himpunan bilangan bulat positif lebih kecil dari 8
A = { x | x  bilangan bulat positif lebih kecil dari  8} atau A  =  { x | x  P, x < 8 } yang ekivalen dengan A = {1, 2, 3, 4, 5, 6, 7}   

 
4. Diagram Venn 

Dalam diagram venn, himpunan semesta S digambarkan dengan persegi panjang, sedangkan untuk himpunan lainnya digambarkan dengan lengkungan tertutup sederhana, dan anggotanya digambarkan dengan noktah. Anggota dari suatu himpunan digambarkan dengan noktah yang terletak di dalam di dalam daerah lengkungan tertutup sederhana itu, atau di dalam persegi panjang untuk anggota yang tidak termasuk di dalam himpunan itu. 

Contoh

S = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}

A = {1, 2, 5}

B = {3, 4, 7, 8}

1.3 Macam Macam Himpunan

1.Himpunan berhingga adalah suatu himpunan yang jumlah anggotanya dapat dihitung.
Contohnya D adalah himpunan bilangan genap kurang dari 10, D ={2,4,6,8}

2. Himpunan tak hingga adalah suatu himpunan yang jumlah anggotanya tidak terbatas atau tak hingga. Contohnya: A adalah himpunan bilangan ganjil, A={1,3,5,7,9,11,.....}

3. Himpunan kosong adalah suatu himpunan yang tidak memiliki anggota sama sekali. Himpunan kosong dilambangkan dengan tanda {}.
Contohnya B = {bilangan genap antara 2 dan 4}. ditulis B={}={0}.

4. Himpunan ekuivalen/himpunan sama adalah himpunan yang anggotanya sama
   contohnya B={merah,kuning,hijau} C={hijau,merah,kuning}, B=C

5. Himpunan semesta adalah himpunan dari semua unsur yang sedang dibicarakan. Himpunan semesta juga disebut himpunan uiversal dan ditulis dengan huruf S.
contohnya:A = {1,3,5,7,9}
himpunan semestanya berupa:
S = {bilangan asli}
S = {bilangan cacah}
S = {bilangan ganjil kurang dari 10}

6.Himpunan bilangan cacah adalah himpunan bilangan yang anggotanya dimulai dari nol dan seterusnya. 

Contoh K = {0,1,2,3,4,5...}

7. Himpunan bagian adalah apabila setiap unsur dalam himpunan B termasuk juga anggota A, maka B merupakan bagian dari himpunan A. 

Contohnya B = {besar}  A = {kecil,sedang,besar} jadi B bagian dari A.

8. Himpunan lepas adalah ssuatu himpunan yang tidak mempunyai anggota persekutuan dengan himpunan lain. 

Contohnya A = {senin,selasa} B = {rabu,kamis,jumat} 

maka himpunan A tidak mempunyai anggota persekutuan dengan himpunan B

9.Himpunan bilangan asli adalah himpunan bilangan yang anggotanya dimulai dari bilangan satu dan seterusnya.

Contohnya D = {1,2,3,4,...}

10. Himpunan bilangan genap adalah himpunan yang anggotanya dimulai dari angka dua dan selalu genap atau habis dibagi dua.

Contohnya G = {2,4,6,8,10,12,...}

11. Himpunan bilangan ganjil adalah himpunan yang anggota bilanganya tidak habis dibagi dua 

Contohnya K = {1,3,5,7...}

12. Himpunan bilangan prima adalah himpunan bilangan yang anggotanya semua bilangan yang memiliki dua faktor. 

Contohnya Y = {2,3,5,7,11,...}

13. Himpunan kuadrat bilangan cacah adalah himpunan bilangan cacah yang anggotanya dipangkatkan dua. 

Contohnya Y = {0^2,1^2,3^2,..)

Semoga bermanfaat ya guys:)

Wassalamualaikum Warahmatullahi Wabarakatuh