TREE(POHON)

Assalamualaikum Warahmatullahi Wabarakatuh

TREE (POHON)

1.1 Definisi

Pohon adalah graf tak-berarah terhubung yang tidak mengandung sirkuit

Hutan (forest) adalah

-     kumpulan pohon yang saling lepas, atau

-     graf tidak terhubung yang tidak mengandung sirkuit. Setiap komponen di dalam graf terhubung tersebut adalah pohon.  

                                          Hutan yang terdiri dari tiga buah pohon

1.2 Pohon Merentang (Spanning Tree)

·         Pohon merentang dari graf terhubung adalah upagraf merentang yang berupa pohon.

·         Pohon merentang diperoleh dengan memutus  sirkuit di dalam graf.

·         Setiap graf terhubung mempunyai paling sedikit satu buah pohon merentang.

·         Graf tak-terhubung dengan k komponen mempunyai k buah hutan merentang yang disebut hutan merentang (spanning forest).

1.3 Graf Merentang Minimum

·         Graf terhubung-berbobot mungkin mempunyai lebih dari 1 pohon merentang.

·         Pohon merentang yang berbobot minimum –dinamakan pohon merentang minimum (minimum spanning tree).

Algoritma Prim

Langkah 1: ambil sisi dari graf G yang berbobot minimum,  masukkan ke dalam T.

Langkah 2:  pilih sisi (u, v) yang mempunyai bobot minimum dan bersisian dengan simpul di T, tetapi (u, v) tidak membentuk sirkuit di T. Masukkan (u, v) ke dalam T.

Langkah 3:  ulangi langkah 2 sebanyak n – 2 kali.

Contoh :

Pohon merentang minimum yang dihasilkan: 

            Bobot = 10 + 25 + 15 + 20 + 35 = 105

·         Pohon merentang yang dihasilkan tidak selalu unik meskipun bobotnya tetap sama.

·         Hal ini terjadi jika ada beberapa sisi yang akan dipilih berbobot sama.

Contoh :

 Tiga buah pohon merentang minimumnya :

Algoritma Kruskal

 ( Langkah 0: sisi-sisi dari graf sudah diurut menaik berdasarkan bobotnya – dari bobot kecil ke bobot besar)

Langkah 1:  T masih kosong

Langkah 2: pilih sisi (u, v) dengan bobot minimum yang tidak membentuk  sirkuit di T. Tambahkan (u, v) ke dalam T.

Langkah 3:   ulangi langkah 2 sebanyak n – 1 kali.

Contoh :

Sisi-sisi diurut menaik :

Pohon merentang minimum yang dihasilkan: 

            Bobot = 10 + 25 + 15 + 20 + 35 = 105

1.4 Pohon Berakar (Rooted Tree)

·         Pohon yang satu buah simpulnya diperlakukan sebagai akar dan sisi-sisinya diberi arah sehingga menjadi graf berarah dinamakan pohon berakar (rooted tree).

Pohon dan dua buah pohon berakar yang dihasilkan dari pemilihan

dua simpul berbeda sebagai akar

1.5 Terminologi pada Pohon Berakar

1. Anak (child atau children) dan Orangtua (parent)

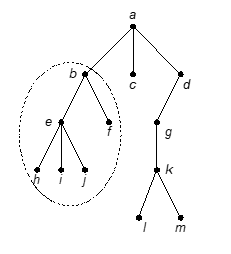
     b, c, dan d adalah anak-anak simpul a,

     a adalah orangtua dari anak-anak itu

2. Lintasan (path)

Lintasan dari a ke j adalah a, b, e, j.

Panjang lintasan dari a ke j adalah 3.

3. Saudara kandung (sibling)

f adalah saudara kandung e, tetapi g bukan

saudara kandung e, karena orangtua mereka

berbeda.

4. Upapohon (subtree)

5. Derajat (degree)

Derajat sebuah simpul adalah jumlah upapohon (atau jumlah anak) pada simpul tersebut.

Derajat a adalah 3, derajat b adalah 2,

Derajat d adalah satu dan derajat c adalah 0.

Jadi, derajat yang dimaksudkan di sini adalah derajat-keluar.

Derajat maksimum dari semua simpul merupakan derajat pohon itu sendiri. Pohon di atas berderajat 3

6. Daun (leaf)

Simpul yang berderajat nol (atau tidak mempunyai anak) disebut daun. Simpul h, i, j, f, c, l, dan m adalah daun.

 

7. Simpul Dalam (internal nodes)

Simpul yang mempunyai anak disebut simpul dalam. Simpul b, d, e, g, dan k adalah simpul dalam.

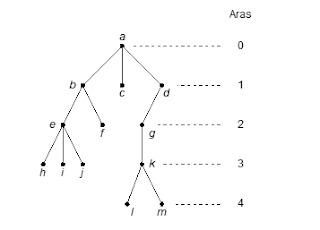
8. Aras (level) atau Tingkat

9. Tinggi (height) atau Kedalaman (depth)

Aras maksimum dari suatu pohon disebut tinggi atau kedalaman pohon tersebut. Pohon di atas mempunyai tinggi 4.

1.6 Pohon Terurut (Ordered Tree)

Pohon berakar yang urutan anak-anaknya penting disebut pohon terurut (ordered tree).

(a) dan (b) adalah dua pohon terurut yang berbeda

Terima Kasih:)

Semoga bermanfaat

Waalaikumsalam Warahmatullahi Wabarakatuh