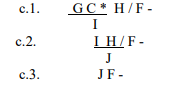TREE (POHON) #2

Assalamu'alaikum Warahmatullahi Wabarakatuh

TREE (POHON) #2

INFIX,POSTFIX dan PREFIX

Ada tiga bentuk penulisan notasi matematis di komputer, satu bentuk adalah yang umum digunakan manusia (sebagai input di komputer) yaitu infix, dan dua yang digunakan oleh komputer (sebagai proses), yaitu postfix dan infix. Berikut contoh-contohnya:

1. Konversi Infix ke Postfix

Untuk mengetahui bentuk postfix dari notasi infix, ada tiga cara yang dapat dilakukan, yaitu (1) manual, (2) stack, dan (3) binary tree. Berikut contoh notasi infixnya:

A * ( B + C ) / D ^ E – F

1.a. Cara Manual

Caranya adalah dengan menyederhanakan notasi menjadi dua operand (variabel) dan satu operator, seperti A + B.

Langkah 1:

tentukan (berdasarkan derajat operasi) mana yang akan diproses terlebih dulu. Diperoleh ( B + C ). Jika ( B + C ) dianggap G, maka notasi infix tadi menjadi: A * G / D ^ E – F

Langkah 2:

dari hasil langkah 1, disederhanakan lagi, kali ini ((berdasarkan derajat operasi) akan disederhanakan D ^ E. Bila D ^ E dianggap H, maka notasi infix tadi menjadi: A * G / H – F

Langkah 3:

dari hasil langkah 2, disederhanakan lagi, kali ini ((berdasarkan derajat operasi) akan disederhanakan A * G. Bila A* G dianggap I, maka notasi infix tadi menjadi: I / H – F

Langkah 4:

dari hasil langkah 3, disederhanakan lagi, kali ini ((berdasarkan derajat operasi) akan disederhanakan I / H. Bila I / H dianggap J, maka notasi infix tadi menjadi: J – F Setelah diperoleh bentuk seperti itu, maka satu per satu kita kembalikan ke notasi semula sambil mengubahnya menjadi notasi postfix.

Langkah 5:

hasil akhir J – F, dibentuk postfixnya, menjadi J F –

Langkah 6:

J sebenarnya adalah I / H yang jika ditulis dalam bentuk postfix menjadi I H /, lalu kita gabung dengan hasil di langkah 5 tadi, diperoleh: I H / F –

Langkah 7:

H sebenarnya adalah D ^ E yang jika ditulis dalam bentuk postfix menjadi D E ^, lalu kita gabung dengan hasil di langkah 6 tadi, diperoleh: I D E ^ / F –

Langkah 8:

I sebenarnya adalah A * G yang jika ditulis dalam bentuk postfix menjadi A G *, lalu kita gabung dengan hasil di langkah 7 tadi, diperoleh: A G * D E ^ / F –

Langkah 9:

G sebenarnya adalah B + C yang jika ditulis dalam bentuk postfix menjadi B C +, lalu kita gabung dengan hasil di langkah 8 tadi, diperoleh: A B C + * D E ^ / F –

Dengan demikian, untuk notasi infix: A * ( B + C ) / D ^ E – F maka notasi postfixnya menjadi: A B C + * D E ^ / F –

Postfix tidak memerlukan tanda kurung, prosesnya berjalan sebagai berikut:

Sama hasilnya pada infix: 2 * ( 3 + 5 ) / 4 ^ 2 – 3 = -2

1.b. Cara Stack

Stack adalah tumpukan (jadi, memori diibaratkan dengan tumpukan) yang memiliki cara kerja, “yang pertama masuk ke kotak, maka akan terakhir kali diambil kembali” atau “first in last out”, atau sebaliknya, “yang terakhir masuk ke kotak, akan diambil yang pertama kali,” atau “last in first out.”

Berikut ini langkah-langkahnya:

1. Proses akan dilakukan dari kiri ke kanan

2. Bila yang diproses adalah operand, maka tulis di hasil. Di sini operand “A”:

A * ( B + C ) / D ^ E – F

3. Lanjutkan ke operator “*”, karena stack masih dalam keadaan kosong, maka masukkan operator tersebut ke dalam stack;

A * ( B + C ) / D ^ E – F

4. Lanjutkan ke operator “(“, operator ini masukkan (tumpuk) saja ke dalam stack;

A * ( B + C ) / D ^ E – F

 

5. Lanjutkan ke operand “B”, karena sebagai operand, maka “B” dijadikan hasil saja.

A * ( B + C ) / D ^ E – F

6. Lanjutkan ke operator “+”, operator ini masukkan (tumpuk) saja ke dalam stack;

A * ( B + C ) / D ^ E – F

Bila top stack (posisi teratas tumpukan) adalah “(“ maka apapun operator yang sedang diproses, masukkan saja ke dalam stack.

7. Lanjutkan ke operand “C”, karena sebagai operand, maka “C” dijadikan hasil saja.

A * ( B + C ) / D ^ E – F

8. Lanjutkan ke operator “)“, operator ini akan mengeluarkan seluruh isi stack (mulai dari atas) hingga bertemu operator “(“ yang menjadi pasangannya. Karena di antara “(“ dan “)” hanya ada “+” maka “+” saja yang dijadikan hasil. Tanda kurung dibuang saja.

A * ( B + C ) / D ^ E – F

9. Lanjutkan ke operator “/“, operator ini akan dimasukkan ke dalam stack. Karena di top stack sudah ada isinya, maka bandingkan keduanya. Bila yang akan masuk memiliki derajat yang lebih besar, maka tumpuk saja. Sebaliknya, bila yang akan masuk memiliki derajat yang sama atau lebih kecil, maka keluarkan top stack hingga operator yang berada di top stack berderajat lebih kecil dari operator yang akan masuk.

Karena “/” berderajat sama dengan “*” maka keluarkan top stack (“*”). Karena stack sudah hampa, maka operator “/” dimasukkan ke dalam stack sebagai top stacknya.

A * ( B + C ) / D ^ E – F

10. Lanjutkan ke operand “D”, karena sebagai operand, maka “D” dijadikan hasil saja.

A * ( B + C ) / D ^ E – F

11. Lanjutkan ke operator “^“, operator ini akan dimasukkan ke dalam stack. Karena di top stack sudah ada isinya, maka bandingkan keduanya. Karena “^” berderajat lebih besar dari top stacknya (“/”) maka masukkan (tumpuk) saja.

A * ( B + C ) / D ^ E – F

12. Lanjutkan ke operand “E”, karena sebagai operand, maka “E” dijadikan hasil saja.

A * ( B + C ) / D ^ E – F

13. Lanjutkan ke operator “-“, operator ini akan dimasukkan ke dalam stack. Karena di top stack sudah ada isinya, maka bandingkan keduanya. Karena “-“ berderajat lebih kecil dari “^” maka operator “^” dikeluarkan dari tumpukan dan dijadikan hasil.

Ketika “-“ akan masuk, di top stack kini ada “/” yang berderajat lebih besar dari “-“, akibatnya top stack (“/”) dikeluarkan juga dan dijadikan hasil. Kini “-“ menjadi top stacknya.

A * ( B + C ) / D ^ E – F

14. Lanjutkan ke operand “F”, karena sebagai operand, maka “F” dijadikan hasil saja.

A * ( B + C ) / D ^ E – F

15. Karena proses telah selesai, maka keluarkan seluruh isi stack mengikuti kaidahnya, last in first out. Karena hanya ada “-“ maka hasil akhirnya menjadi:

A B C + * D E ^ / F –

Hasil ini harus sama dengan postfix yang menggunakan cara manual. Terlihat langkahnya lebih panjang dari cara manual, namun jika telah terbiasa, cara ini dapat dilakukan dengan lebih mudah dari pada cara manual. Kalau dipersingkat, bentuknya menjadi:

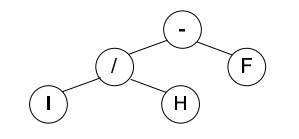
1.c. Cara Binary Tree

1. Langkah pertama untuk mengkonversi notasi infix menjadi postfix adalah dengan membuat struktur pohon binarnya. Langkah pertama untuk membuat struktur pohonnya adalah dengan menyederhanakan notasi seperti yang pernah dilakukan di cara manual hingga langkah 4, yaitu: J – F yang struktur pohon binarnya adalah:

2. Jabarkan J, yaitu I / H yang struktur pohon binarnya adalah:

Letakkan struktur pohon binar J ini ke struktur pohon binar yang sudah dibentuk di langkah 1 tadi, jadi, struktur pohon binarnya menjadi:

3. Jabarkan I, yaitu A * G. Sama dengan langkah 2, maka struktur pohon binarnya menjadi:

4. Jabarkan G, yaitu B + C. Sama caranya dengan langkah 2, maka struktur pohon binarnya menjadi:

5. Jabarkan H, yaitu D ^ E. Sama caranya dengan langkah 2, maka struktur pohon binarnya menjadi:

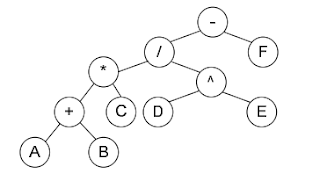
Inilah struktur pohon binar terakhir untuk notasi A * ( B + C ) / D ^ E – F

Lalu, bagaimana menentukan notasi postfixnya ?. Tinggal mengikuti gerakan perjalanan atau kunjungan (traversal) secara post-order saja, yaitu rekursif dari (left-right-root) atau ulangi(kiri, kanan, tengah).

a. Paling kiri adalah A, jadi hasil = A

b. Setelah kiri, kita ke kanan dari A, diperoleh +. Ulangi proses lagi, yang paling kiri adalah B, jadi hasil = A B

c. Setelah kiri, kita ke kanan dari B, diperoleh C. Karena C merupakan ujung pohon (daun), maka jadikan hasil. Jadi, hasil = A B C

d. Dari kanan (C) kita ke tengah, diperoleh tanda +. Karena di kiri dan kanan + sudah diproses, maka jadikan + sebagai hasil. Jadi, hasil = A B C +

e. Kembali ke tengah dari struktur pohon A * +, kita peroleh *. Karena di kiri dan kanan lambang * sudah diproses, maka jadikan * sebagai hasil. Jadi, hasilnya: A B C + *

f. Kembali ke tengah struktur dari * / ^, yaitu /. Di kiri lambang / sudah diproses, maka kita ke kanan, sehingga diperoleh ^. Dari sini proses kembali diulang, kiri dari ^ adalah D yang merupakan daun dari struktur pohon itu. Jadi, hasil = A B C + * D

g. Setelah kiri, kita ke kanan. Diperoleh E, jadi hasilnya = A B C + * D E

h. Setelah kanan, kita kembali ke tengah, diperoleh ^, sehingga hasilnya menjadi A B C + * D E ^

i. Kita kembali ke tengah sebelumnya, yaitu /. Karena di kiri dan kanan lambang / sudah diproses, maka lambang / menjadi hasil. Jadi, hasil = A B C + * D E ^ /

j. Di kiri dan kanan lambang / sudah diproses, kita kembali ke root (akar, puncak struktur pohon binar), yaitu -. Di kiri lambang – sudah diproses semua, maka kita ke kanan, diperoleh F yang merupakan daun. Hasilnya menjadi A B C + * D E ^ / F

k. Terakhir, kita kembali ke puncak (yang merupakan lambang terakhir dalam postfix), hasilnya = A B C + * D E ^ / F –

Berikut skema pergerakannya:

2. Konversi Infix ke Prefix

Cara mengonversi infix ke prefix dapat dilakukan dengan dua cara, yaitu (a) manual, dan (b) binary tree.

2.a. Cara Manual

Dengan soal yang sama, maka cara manual mengonversi notasi infix ke prefix dimulai sama dengan cara di sub-bab 1.a. proses 1 sampai 4, hingga diperoleh: J – F.

Langkah 1:

J – F dalam notasi prefix ditulis dengan - J F

Langkah 2:

J adalah I / H yang notasi prefixnya adalah / I H, sehingga ketika digabung akan menjadi - / I H F

Langkah 3:

I adalah A * G yang notasi prefixnya adalah * A G, sehingga ketika digabung akan menjadi - / * A G H F

Langkah 4:

G adalah (B + C) yang notasi prefixnya adalah + B C, sehingga ketika digabung akan menjadi - / * A + B C H F

Langkah 5:

H adalah D ^ E yang notasi prefixnya adalah ^ D E, sehingga ketika digabung akan menjadi - / * A + B C ^ D E F

Jadi, untuk notasi infix: A * ( B + C ) / D ^ E – F, maka notasi postfix adalah: - / * A + B C ^ D E F

2.b. Cara Binary Tree

Caranya sama dengan cara binary tree sebelumnya. Singkatnya, setelah struktur pohonnya terbentuk, maka berikut ini traversalnya secara pre-order dengan rumus: rekursif(tengah, kiri, kanan), atau rekursif (root, left, right) sebagai berikut:

3. Konversi Prefix ke Infix dan/atau Postfix

Konversi dari prefix ke infix dan/atau postfix bisa dilakukan melalui bantuan manual atau pohon binar. Contoh: notasi prefix: - / * + A B C^ D E F, maka notasi infixnya adalah:

a.       Langkah I: cari yang bentuknya: + A B (operator, operand, operand). Diperoleh:

b.      Sederhanakan notasi tersebut menjadi: - / * G C H F

c.       Ulangi langkah I hingga menjadi satu operator dan dua operand:

d.      Jadikan bentuk infix dan kembalikan ke notasi semula (setiap penjabaran diberi tanda kurung):

1)    J – F

2)    J = (I / H), digabung menjadi: (I / H) – F

3)    H = (D ^ E), digabung menjadi: (I / (D ^ E)) – F

4)    I = (G * C), digabung menjadi: ((G * C) / (D ^ E)) – F

5)    G = (A + B), digabung menjadi (((A + B) * C) / (D ^ E)) - F

Dengan cara yang sama, kita bisa mengalihkan notasi prefix tersebut ke notasi postfixnya, yaitu:

a.       Langkah I: cari yang bentuknya: + A B (operator, operand, operand). Diperoleh:

b.      Sederhanakan notasi tersebut menjadi: - / * G C H F

c.       Ulangi langkah I hingga menjadi satu operator dan dua operand:

d.      Jadikan bentuk postfix dan kembalikan ke notasi semula:

1)    – J F pada prefix menjadi J F - dalam postfix

2)    J = I H / , digabung menjadi: I H / F –

3)    H = D E ^, digabung menjadi: I D E ^ / F –

4)    I = G C *, digabung menjadi: G C * D E ^ / F –

5)    G = A B +, digabung menjadi A B + C * D E ^ / F –

Dengan cara yang sama pula, mari kita bentuk struktur pohon binarnya.

- JF, pohon binarnya adalah:

J = I H /, sehingga pohonnya menjadi:

H = D E ^, sehingga pohonnya menjadi:

I = G C *, sehingga pohonnya menjadi:

G = A B +, maka pohonnya menjadi:

4. Konversi Postfix ke Infix dan/atau Prefix

Sama caranya dengan konversi dari prefix ke infix dan/atau postfix, konversi postfix ke infix atau prefix bisa dilakukan melalui bantuan manual atau pohon binar. Contoh: notasi postfix: A B + C * D E ^ / F -, maka notasi infixnya adalah:

a.       Langkah I: cari yang bentuknya: A B + (operand, operand, operator). Diperoleh:

b.      Sederhanakan notasi tersebut menjadi: G C * H / F –

c.       Ulangi langkah I hingga menjadi satu operator dan dua operand:

d.      Jadikan bentuk infix dan kembalikan ke notasi semula (setiap penjabaran diberi tanda kurung):

1)    J F – jadi ( J – F )

2)    J = (I / H), digabung menjadi: (I / H) – F

3)    H = (D ^ E), digabung menjadi: (I / (D ^ E)) – F

4)    I = (G * C), digabung menjadi: ((G * C) / (D ^ E)) – F

5)    G = (A + B), digabung menjadi (((A + B) * C) / (D ^ E)) - F

Dengan cara yang sama, kita bisa mengalihkan notasi postfix tersebut ke notasi prefixnya, yaitu:

a.       Langkah I: cari yang bentuknya: A B + (operand, operand, operator). Diperoleh:

b.      Sederhanakan notasi tersebut menjadi: G C * H / F –

c.       Ulangi langkah I hingga menjadi satu operator dan dua operand:

d.      Jadikan bentuk prefix dan kembalikan ke notasi semula:

1)    J F - pada postfix menjadi - J F dalam pretfix

2)    J = / I H , digabung menjadi: - / I H F –

3)    H = ^ D E, digabung menjadi: - / I ^ D E F –

4)    I = G C *, digabung menjadi: - / * G C ^ D E F –

5)    G = A B +, digabung menjadi - / * + A B C ^ D E F –

Dengan cara yang sama pula, mari kita bentuk struktur pohon binarnya.

J F -, pohon binarnya adalah:

J = / I H/, sehingga pohonnya menjadi:

H = ^ D E, sehingga pohonnya menjadi:

I = * G C, sehingga pohonnya menjadi:

G = + A B, maka pohonnya menjadi:

Terima Kasih:)

Wassalamualaikum Warahmatullahi Wabarakatuh

TREE(POHON)

Assalamualaikum Warahmatullahi Wabarakatuh

TREE (POHON)

1.1 Definisi

Pohon adalah graf tak-berarah terhubung yang tidak mengandung sirkuit

Hutan (forest) adalah

-     kumpulan pohon yang saling lepas, atau

-     graf tidak terhubung yang tidak mengandung sirkuit. Setiap komponen di dalam graf terhubung tersebut adalah pohon.  

                                          Hutan yang terdiri dari tiga buah pohon

1.2 Pohon Merentang (Spanning Tree)

·         Pohon merentang dari graf terhubung adalah upagraf merentang yang berupa pohon.

·         Pohon merentang diperoleh dengan memutus  sirkuit di dalam graf.

·         Setiap graf terhubung mempunyai paling sedikit satu buah pohon merentang.

·         Graf tak-terhubung dengan k komponen mempunyai k buah hutan merentang yang disebut hutan merentang (spanning forest).

1.3 Graf Merentang Minimum

·         Graf terhubung-berbobot mungkin mempunyai lebih dari 1 pohon merentang.

·         Pohon merentang yang berbobot minimum –dinamakan pohon merentang minimum (minimum spanning tree).

Algoritma Prim

Langkah 1: ambil sisi dari graf G yang berbobot minimum,  masukkan ke dalam T.

Langkah 2:  pilih sisi (u, v) yang mempunyai bobot minimum dan bersisian dengan simpul di T, tetapi (u, v) tidak membentuk sirkuit di T. Masukkan (u, v) ke dalam T.

Langkah 3:  ulangi langkah 2 sebanyak n – 2 kali.

Contoh :

Pohon merentang minimum yang dihasilkan: 

            Bobot = 10 + 25 + 15 + 20 + 35 = 105

·         Pohon merentang yang dihasilkan tidak selalu unik meskipun bobotnya tetap sama.

·         Hal ini terjadi jika ada beberapa sisi yang akan dipilih berbobot sama.

Contoh :

 Tiga buah pohon merentang minimumnya :

Algoritma Kruskal

 ( Langkah 0: sisi-sisi dari graf sudah diurut menaik berdasarkan bobotnya – dari bobot kecil ke bobot besar)

Langkah 1:  T masih kosong

Langkah 2: pilih sisi (u, v) dengan bobot minimum yang tidak membentuk  sirkuit di T. Tambahkan (u, v) ke dalam T.

Langkah 3:   ulangi langkah 2 sebanyak n – 1 kali.

Contoh :

Sisi-sisi diurut menaik :

Pohon merentang minimum yang dihasilkan: 

            Bobot = 10 + 25 + 15 + 20 + 35 = 105

1.4 Pohon Berakar (Rooted Tree)

·         Pohon yang satu buah simpulnya diperlakukan sebagai akar dan sisi-sisinya diberi arah sehingga menjadi graf berarah dinamakan pohon berakar (rooted tree).

Pohon dan dua buah pohon berakar yang dihasilkan dari pemilihan

dua simpul berbeda sebagai akar

1.5 Terminologi pada Pohon Berakar

1. Anak (child atau children) dan Orangtua (parent)

     b, c, dan d adalah anak-anak simpul a,

     a adalah orangtua dari anak-anak itu

2. Lintasan (path)

Lintasan dari a ke j adalah a, b, e, j.

Panjang lintasan dari a ke j adalah 3.

3. Saudara kandung (sibling)

f adalah saudara kandung e, tetapi g bukan

saudara kandung e, karena orangtua mereka

berbeda.

4. Upapohon (subtree)

5. Derajat (degree)

Derajat sebuah simpul adalah jumlah upapohon (atau jumlah anak) pada simpul tersebut.

Derajat a adalah 3, derajat b adalah 2,

Derajat d adalah satu dan derajat c adalah 0.

Jadi, derajat yang dimaksudkan di sini adalah derajat-keluar.

Derajat maksimum dari semua simpul merupakan derajat pohon itu sendiri. Pohon di atas berderajat 3

6. Daun (leaf)

Simpul yang berderajat nol (atau tidak mempunyai anak) disebut daun. Simpul h, i, j, f, c, l, dan m adalah daun.

 

7. Simpul Dalam (internal nodes)

Simpul yang mempunyai anak disebut simpul dalam. Simpul b, d, e, g, dan k adalah simpul dalam.

8. Aras (level) atau Tingkat

9. Tinggi (height) atau Kedalaman (depth)

Aras maksimum dari suatu pohon disebut tinggi atau kedalaman pohon tersebut. Pohon di atas mempunyai tinggi 4.

1.6 Pohon Terurut (Ordered Tree)

Pohon berakar yang urutan anak-anaknya penting disebut pohon terurut (ordered tree).

(a) dan (b) adalah dua pohon terurut yang berbeda

Terima Kasih:)

Semoga bermanfaat

Waalaikumsalam Warahmatullahi Wabarakatuh