GRAF
1.1 Definisi
Graf
Graf merupakan struktur diskrit
yang terdiri himpunan sejumlah berhingga obyek yang disebut simpul (vertices,
vertex) dan himpunan sisi (edges) yang menghubungkan simpul-simpul terseut.
terdiri dari dari Graf digunakan untuk merepresentasikan objekobjek diskrit dan
hubungan antara objek-objek tersebut.
Notasi sebuah graf adalah G = (V, E),
dimana :
· V merupakan himpunan tak kosong dari
simpul-simpul (vertices), misalkan V = { v1 , v2 , ... , vn }
· E merupakan himpunan sisi – sisi (edges) yang
menghubungkan sepasang simpul, misalkan
E = {e1 , e2 , ... , en }
Contoh :
Graf dari masalah jembatan Königsberg dapat
disajikan sebagai berikut :
Misalkan graf tersebut adalah G(V, E) dengan
V = { A, B,
C, D }
E = { (A,
C), (A, C), (A, B), (A, B), (B, D), (A, D), (C, D)}
= { e1, e2, e3, e4, e5, e6, e7}
Pada graf tersebut sisi e1 = (A,
C) dan sisi e2 = (A, C) dinamakan sisi-ganda (multiple edges atau paralel
edges) karena kedua sisi ini menghubungi dua buah simpul yang sama, yaitu
simpul A dan simpul C. Begitu pun dengan sisi e3 dan sisi e4. Sementara itu,
pada graf diatas, tidak terdapat gelang (loop), yaitu sisi yang berawal dan
berakhir pada simpul yang sama.
Dari definisi graf, himpunan sisi
(E) memungkinkan berupa himpunan kosong. Jika graf tersebut mempunyai himpunan
sisi yang merupakan himpunan kosong maka graf tersebut dinamakan graf kosong
(null graph atau empty graph).
Contoh :
Graf
kosong dengan 3 simpul (graf N3 )
Dengan memperhatikan kondisi
sisinya, suatu graf dapat dikategorikan sebagai graf tidak berarah dan graf
berarah. Graf tidak berarah, seperti telah dijelaskan pada contoh graf untuk
jembatan Königsberg. Sementara itu, graf berarah (directed graph, digraph)
merupakan graf yang mempunyai sisi yang berarah, artinya satu buah simpul yang
dihubungkan oleh sisi tersebut merupakan simpul awal (initial vertex) dan
simpul yang lain dikatakan sebagai simpul akhir (terminal vertex).
Contoh :
Graf
berikut merupakan graf berarah :
Terlihat bahwa
e1 = (P, S), e3 = (R, Q), dan e5 = (Q, Q) R
Simpul P
merupkan simpul awal bagi sisi e1 dan simpul S merupakan simpul akhir bagi sisi
e1.
1.2 Terminologi Graf
Ada beberapa terminologi graf
yang perlu diketahui, antara lain : ketetanggaan antara dua simpul, bersisian ,
derajat suatu simpul, dan lain-lain. Berikut ini adalah beberapa terminoogi
yang penting, yaitu :
1. Bertetangga (Adjacent)
Dua buah
simpul dikatakan bertetangga jika kedua simpul tersebut terhubung langsung oleh
suatu sisi.
Contoh :
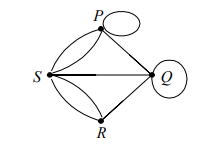
Perhatikan
graf berikut :
Pada graf
diatas : simpul P bertetangga dengan simpul Q dan S, tetapi simpul P tidak
bertetangga dengan simpul R.
2. Bersisian
(Incidency)
Suatu sisi e
dikatakan bersisian dengan simpul v1 dan simpul v2 jika e menghubungkan kedua
simpul tersebut, dengan kata lain e = (v1, v2).
Contoh :
Perhatikan
graf dari masalah jembatan Königsberg berikut ini :
maka e1
bersisian dengan simpul A dan simpul C , tetapi sisi tersebut tidak berisian
dengan simpul B.
3. Simpul Terpencil (Isolated Vertex)
Jika suatu
simpul tidak mempunyai sisi yang bersisian dengannya maka simpul tersebut
dinamakan simpul terpencil.
Contoh :
Perhatikan
graf berikut :
Simpul T dan
simpul U merupakan simpul terpencil.
4. Derajat
(Degree)
Derajat suatu
simpul merupakan jumlah sisi yang bersisian dengan simpul tersebut. Misalkan,
suatu simpul v mempunyai 3 buah sisi yang bersisian dengannya maka dapat
dikatakan simpul tersebut berderajat 3, atau dinotasikan oleh d(v) = 3.
Contoh :
Perhatikan
graf berikut :
Pada graf
diatas : d(P) = d(Q) = d (S)= 5, sedangkan d(R) = 3.
Derajat sebuah
simpul pada suatu graf berarah dijelaskan sebagai berikut :
·
din(v) merupakan jumlah busur yang masuk
ke simpul v
·
dout(v) merupakan jumlah busur yang keluar
dari simpul v
Dengan
demikian derajat pada simpul tersebut, diperoleh : d(v) = din(v)
+ dout(v)
5. Lintasan (Path)
Lintasan dari
suatu simpul awal v0 ke simpul tujuan vT di dalam suatu graf G merupakan
barisan sebuah sisi atau lebih (x0, x1), (x1, x2), (x2, x3), …, (xn-1, xn) pada
G, dimana x0 = v0 dan xn = vT. Lintasan ini dinotasikan oleh :
x0, x1, x2,
x3, …, xn
Lintasan ini
mempunyai panjang n, karena lintasan ini memuat n buah sisi, yang dilewati dari
suatu simpul awal v0 ke simpul tujuan vT di dalam suatu graf G. Suatu lintasan
yang berawal dan berakhir pada simpul yang sama dinamakan Siklus (Cycle) atau
Sirkuit (Circuit).
Contoh :
Perhatikan
graf berikut ini :
- · Pada graf tersebut lintasan P, Q, R memiliki panjang 2. Sementara itu lintasan P, Q, S, R memiliki panjang 3.
- · Lintasan P, Q, R, S, P dinamakan siklus atau sirkuit dengan panjang 4.
- · Antara simpul P dan U maupun T tidak dapat ditemukan lintasan.
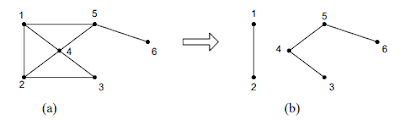
6. Cut-Set
Cut-set dari
suatu graf terhubung G adalah himpunan sisi yang jika dibuang dari G
menyebabkan G tidak terhubung. Jadi, cut-set selalu menghasilkan dua buah
subgraf . Pada graf di bawah, {(1,4), (1,5), (2, 3), (2,4)} adalah cut-set.
Terdapat banyak cut-set pada sebuah graf terhubung. Himpunan {(1,5), (4,5)} juga
adalah cut-set, {(1,4), (1,5), (1,2)} adalah cut-set, {(5,6)} juga cut-set,
tetapi {(1,4),
(1,5), (4,5)} bukan cut-set sebab himpunan bagiannya, {(1,5), (4,5)} adalah
cut-set.
1.3 Beberapa
Jenis Graf
Beberapa jenis graf tak berarah
yang perlu diketahui adalah :
1.
Graf sederhana (simple graph)
Graf sederhana
merupakan graf tak berarah yang tidak mengandung gelang maupun sisi-ganda.
Contoh :
2.
Graf Ganda (multigraph)
Graf ganda
merupakan graf tak berarah yang tidak mengandung gelang (loop).
Contoh :
Dengan
demikian, graf sederhana pun merupakan graf ganda (multi graph).
3.
Graf semu (Pseudo graph)
Graf semu
merupakan graf yang boleh mengandung gelang (loop).
Contoh :
1.4 Graf
Isomorfik dan Homeomorfik
Perhatikan
dua graf berikut ini :
Dua buah graf
diatas, terdiri dari empat buah simpul dimana setiap simpul adalah berderajat
tiga. Walaupun secara geometri kedua tersebut berbeda tetapi pada prinsipnya
kedua graf tersebut adalah sama.
Definisi :
Dua buah graf
G1 dan G2 dikatakan isomorfik jika terdapat korespondensi satu-satu antara
simpul-simpul pada kedua graf tersebut dan antara sisi-sisi keduanya sehingga
jika sisi e bersisian dengan simpul u dan v pada G1 maka sisi e’ pada G2 juga
bersisian dengan simpul u’ dan v’.
Suatu graf
dapat digambarkan dengan berbagai cara. Dua buah graf yang isomorfik adalah
graf yang sama, kecuali penamaan simpul dan sisinya saja yang berbeda. Sebagai
contoh dua graf diatas merupakan dua graf yang isomorfik .
Dua buah graf
dikatakan isomorfik jika memenuhi ketiga syarat berikut (Deo, 1989):
1.
Mempunyai jumlah simpul yang sama.
2.
Mempunyai jumlah sisi yang sama
3.
Mempunyai jumlah simpul yang sama berderajat
tertentu
Tetapi cara
menunjukan dua graf yang isomorfik dapat diperhatikan pada contoh berikut ini.
Contoh :
Diketahui 2
buah graf berarah :
Periksa apakah
kedua graf tersebut isomorfik? Jika ya, tentukan simpul-simpul yang saling
berkorespondensi antara G1 dan G2
Jawab :
Ya, kedua graf
tersebut adalah isomorfik. Terlihat graf tersebut memuat simpul dimana setiap
simpulnya masing-masing berderajat tiga.
Simpul yang saling berkorespondensi dari kedua graf tersebut adalah :
·
Simpul u1 dengan simpul v1
·
Simpul u2 dengan simpul v3
·
Simpul u3 dengan simpul v5
·
Simpul u4 dengan simpul v6
·
Simpul u5 dengan simpul v4
·
Simpul u6 dengan simpul v2
Pada dua graf
yang isomorfik, kedua graf tersebut memiliki matriks ketetanggaan yang sama.
Perhatikan matriks ketetanggaan dari kedua graf tersebut.
Dibawah ini
adalah matriks ketetanggaan dari graf G1 :
Sementara itu,
berikut ini adalah matriks ketetanggaan dari graf G1 :
Terlihat bahwa
kedua graf tersebut memiliki matriks ketetanggaan yang sama, yaitu MG1 = MG2.
Selanjutnya
akan dijelaskan tentang definisi homeomorfik antara dua buah graf. Misalkan
G2(V2, E2) diperoleh dari G1(V1, E1) dengan menambahkan simpul pada sebuah sisi
atau lebih pada graf tersebut, maka graf G1(V1, E1) dan graf G2(V2, E2)
dinamakan homeomorfik.
Contoh :
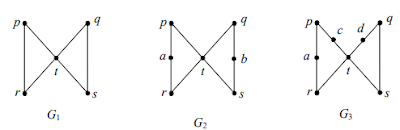
Perhatikan
ketiga graf dibawah ini :
Ketiga graf
diatas merupakan graf homeomorfik (homeomorphic graphs).
1.5 Graf Planar dan Graf Bidang
Graf yang dapat digambarkan pada bidang datar dengan
sisi-sisi tidak saling memotong (bersilangan) disebut graf planar, jika tidak, maka ia disebut graf tak-planar.
K4 adalah graf planar:
K5 adalah graf tidak planar:
Graf planar yang digambarkan dengan sisi-sisi yang tidak
saling berpotongan disebut graf bidang (plane graph).
Tiga buah graf planar. Graf (b) dan (c) adalah graf bidang
1.6 Aplikasi Graf Planar
Persoalan utilitas (utility problem)
(a) Graf persoalan utilitas (K3,3)
(b) Graf persoalan utilitas bukan graf
planar.
· Perancangan
IC (Integrated Circuit)
· Tidak
boleh ada kawat-kawat di dalam ICboard yang saling bersilangan -> dapat
menimbulkan interferensi arus listrik -> malfunction
· Perancangan
kawat memenuhi prinsip graf planar
1.7 Teorema Kuratoswki
Berguna untuk menentukan dengan tegas keplanaran suat
graf.
a) Graf Kuratowski pertama (K5)
b) Graf Kuratowski kedua (K3, 3)
c) Graf yang isomorfik dengan graf
Kuratowski kedua
Sifat graf Kuratowski
adalah:
1. Kedua graf Kuratowski adalah graf
teratur.
2. Kedua graf Kuratowski adalah graf
tidak-planar
3. Penghapusan sisi atau simpul dari
graf Kuratowski menyebabkannya menjadi graf planar.
4. Graf Kuratowski pertama adalah graf
tidak-planar dengan jumlah simpul minimum, dan graf Kuratowski kedua adalah
graf tidak-planar dengan jumlah sisi minimum.
TEOREMA
Kuratowski. Graf G bersifat planar jika dan hanya jika ia tidak mengandung
upagraf yang isomorfik dengan salah satu graf Kuratowski atau homeomorfik
(homeomorphic) dengan salah satu dari keduanya.
Tiga
buah graf yang homemorfik satu sama lain.
1.8 Lintasan
dan Sirkuit Euler
· Lintasan
Euler ialah lintasan yang melalui masing-masing sisi di dalam graf tepat satu
kali.
· Sirkuit
Euler ialah sirkuit yang melewati masing-masing sisi tepat satu kali.
· Graf
yang mempunyai sirkuit Euler disebut graf Euler (Eulerian graph). Graf yang mempunyai
lintasan Euler dinamakan juga graf semi-Euler (semi-Eulerian graph).
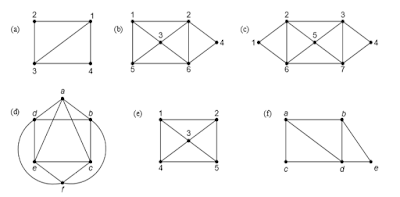
Contoh :
Lintasan Euler pada graf (a) : 3, 1, 2, 3, 4, 1
Lintasan Euler pada graf (b) : 1, 2, 4, 6, 2, 3, 6, 5, 1, 3
Sirkuit Euler pada graf (c)
: 1, 2, 3, 4, 7, 3, 5, 7, 6, 5, 2, 6, 1
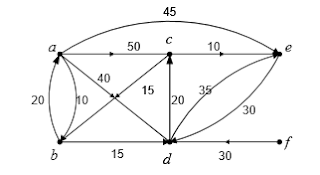
Sirkuit Euler pada graf (d)
: a, c, f, e, c, b, d, e, a, d,
f, b, a
Graf (e) dan (f) tidak mempunyai lintasan maupun sirkuit
Euler
(a) dan (b) graf semi-Euler
(c) dan (d) graf Euler
(e) dan (f) bukan graf semi-Euler atau graf Euler
TEOREMA. Graf tidak berarah memiliki lintasan Euler jika
(graf semi-Euler) dan hanya jika terhubung dan memiliki dua buah simpul
berderajat ganjil atau tidak ada simpul berderajat ganjil sama sekali.
TEOREMA. Graf tidak berarah G adalah graf Euler (memiliki
sirkuit Euler) jika dan hanya jika setiap simpul berderajat genap.
TEOREMA. (a) Graf
berarah G memiliki sirkuit Euler jika dan hanya jika G terhubung dan setiap
simpul memiliki derajat-masuk dan derajat-keluar sama. (b) G memiliki lintasan Euler jika dan hanya
jika G terhubung dan setiap simpul memiliki derajat-masuk dan derajat-keluar
sama kecuali dua simpul, yang pertama memiliki derajat-keluar satu lebih besar
derajat-masuk, dan yang kedua memiliki derajat-masuk satu lebih besar dari
derajat-keluar.
(a) Graf berarah Euler
(a, g, c, b, g, e, d, f, a)
(b) Graf berarah semi-Euler (d, a, b, d, c, b)
(c) Graf berarah bukan Euler maupun semi-Euler.
1.9 Lintasan dan Sirkuit Hamilton
·
Lintasan
Hamilton ialah lintasan yang melalui tiap simpul di dalam graf tepat satu
kali.
· Sirkuit
Hamilton ialah sirkuit yang melalui tiap simpul di dalam graf tepat satu kali,
kecuali simpul asal (sekaligus simpul akhir) yang dilalui dua kali.
· Graf
yang memiliki sirkuit Hamilton dinamakan graf Hamilton, sedangkan graf yang
hanya memiliki lintasan Hamilton disebut graf semi-Hamilton.
(a) graf yang memiliki lintasan
Hamilton (misal: 3, 2, 1, 4)
(b) graf yang memiliki lintasan
Hamilton (1, 2, 3, 4, 1)
(c) graf yang tidak memiliki lintasan
maupun sirkuit Hamilton.
(a) Dodecahedron Hamilton,
(b) graf yang mengandung sirkuit
Hamilton
TEOREMA. Syarat cukup supaya graf sederhana G dengan n
(≥ 3) buah simpul adalah graf Hamilton ialah bila derajat tiap
simpul paling sedikit n/2 (yaitu, d(v) ≥ n/2 untuk setiap simpul v di G).
(coba nyatakan dalam “jika p maka q”)
TEOREMA. Setiap graf lengkap adalah graf Hamilton.
TEOREMA. Di dalam graf lengkap G
dengan n buah simpul (n ≥ 3), terdapat (n – 1)!/2 buah sirkuit
Hamilton.
1.10 Beberapa Aplikasi Graf
a. Lintasan Terpendek (Shortest Path)
Misalkan
G merupakan graf berbobot (weighted graph),
yaitu setiap sisi dari graf G memiliki bobot tertentu, seperti pada
ilustrasi dibawah ini :
Hal
yang biasanya dilakukan adalah menentukan lintasan terpendekpada graf
tersebut. Dengan kata lain, menentukan lintasan yang memiliki total bobot minimum.
Contoh
:
1.
Menentukan jarak terpendek/waktu tempuh tersingkat/ongkos termurah antara dua buah kota
2.
Menentukan waktu tersingkat pengiriman pesan (message) antara dua buah terminal
pada jaringan komputer.
Beberapa
jenis persoalan lintasan terpendek, antara lain
a. Lintasan terpendek antara dua buah
simpul tertentu.
b. Lintasan terpendek antara semua
pasangan simpul.
c. Lintasan terpendek dari simpul
tertentu ke semua simpul yang lain.
d. Lintasan terpendek antara dua buah
simpul yang melalui beberapa simpul tertentu.
Algoritma
Lintasan Terpendek
Dijkstra
Algoritma Dijkstra merupakan suatu algoritma yang digunakan untuk menentukan
lintasan terpendek dari suatu simpul ke semua simpul lain. Untuk mempermudah dalam pemahaman Algoritma
Dijkstra, berikut ini adalah graf dimana simpul-simpulnya merepresentasikan
kota-kota di Amerika Serikat dan sisi dari graf tersebut merepresentasikan
jarak antar dua kota (dalam kilometer).
Contoh
:
Dengan
menggunakan Algoritma Dijkstra akan ditentukan jarak terpendek dari kota Boston
ke kota-kota yang lainnya.
Jadi,
lintasan terpendek dari:
5 ke 6
adalah 5, 6 dengan jarak = 250 km
5 ke 7
adalah 5, 6, 7 dengan jarak = 1150 km
5 ke 4
adalah 5, 6, 4 dengan jarak = 1250 km
5 ke 8
adalah 5, 6, 8 dengan jarak = 1650 km
5 ke 3
adalah 5, 6, 4, 3 dengan jarak = 2450 km
5 ke 2
adalah 5, 6, 4, 3, 2 dengan jarak = 3250 km
5 ke 1
adalah 5, 6, 8, 1 dengan jarak = 3350 km
b. Persoalan Perjalanan Pedagang
(Travelling Salesperson Problem - TSP)
Seperti
halnya contoh pada (a), misalkan diberikan sejumlah kota dan jarak antar kota.
Tentukan sirkuit terpendek yang harus dilalui oleh seorang pedagang bila
pedagang itu berangkat dari sebuah kota asal dan ia harus menyinggahi setiap
kota tepat satu kali dan kembali lagi ke kota asal keberangkatan. Ini merupakan masalah menentukan sirkuit
Hamilton yang memiliki bobot minimum.
c. Persoalan Tukang Pos Cina (Chinese
Postman Problem)
Permasalahan
ini, pertama kali dikemukakan oleh Mei Gan (berasal dari Cina) pada tahun 1962,
yaitu : Seorang tukang pos akan mengantar surat ke alamat-alamat sepanjang
jalan di suatu daerah. Bagaimana ia merencanakan rute perjalanannya supaya ia
melewati setiap jalan tepat sekali dan kembali lagi ke tempat awal
keberangkatan. Permasalahan tersebut
merupakan masalah menentukan sirkuit
Euler di dalam suatu graf.
Terima Kasih
Wassalamualaikum Warahmatullahi Wabarakatuh
Semoga bermanfaat:)